数学算法（数论/组合/概率期望/博弈/计算几何/随机算法）

本文参考灵神的题单，整理了力扣上数学相关的题目，主要以数论和组合数学为主。

部分题目会涉及到取模，参考： 模运算的世界：当加减乘除遇上取模

一、数论

1.1、判断质数

质数的定义：大于1的自然数，除了1和他本身外，不能被其他自然数整除。

模板

Java

class Solution {
    public boolean isPrime(int n) {
        for (int i =2 ; i * i <= n; i++) {
            if (n % i == 0) {
                return false;
            }
        }
        return n >= 2; // 1不是质数
    }
}

Python

# 时间复杂度 O(sqrt(n))
def is_prime(n: int) -> bool:
    for i in range(2, isqrt(n) + 1):
        if n % i == 0:
            return False
    return n >= 2  # 1 不是质数

2614. 对角线上的质数（20250519更新）

Details

给你一个下标从 0 开始的二维整数数组 nums 。

返回位于 nums 至少一条 对角线 上的最大 质数 。如果任一对角线上均不存在质数，返回 0 。

注意：

• 如果某个整数大于 1 ，且不存在除 1 和自身之外的正整数因子，则认为该整数是一个质数。
• 如果存在整数 i ，使得 nums[i][i] = val 或者 nums[i][nums.length - i - 1]= val ，则认为整数 val 位于 nums 的一条对角线上。

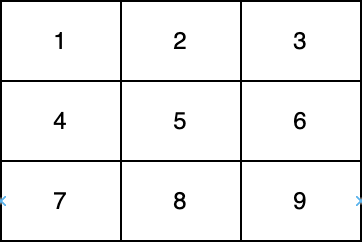
在上图中，一条对角线是 [1,5,9] ，而另一条对角线是 [3,5,7] 。

示例 1：

输入：nums = [[1,2,3],[5,6,7],[9,10,11]]
输出：11
解释：数字 1、3、6、9 和 11 是所有 "位于至少一条对角线上" 的数字。由于 11 是最大的质数，故返回 11 。

示例 2：

输入：nums = [[1,2,3],[5,17,7],[9,11,10]]
输出：17
解释：数字 1、3、9、10 和 17 是所有满足"位于至少一条对角线上"的数字。由于 17 是最大的质数，故返回 17 。

提示：

• 1 <= nums.length <= 300
• nums.length == numsi.length
• 1 <= nums[i][j] <= 4*106

需要解决这个题目，前提是我们是需要知道什么是质数，质数的定义就是：大于1的正整数，只能被1和它本身整除。所以最小的质数是2.

然后需要了解的就是对角线元素的下标，如果使用两层循环的话，i表示行，长度为m，j表示列，长度为n，那么对角线元素就是：i == j 或者是 i == n-j-1;

如果是一层循环的话，i表示行，长度为m，对角线的坐标i == i或者是i == m - i -1。

nums行数和列数相等。

• 使用单层循环找对角线元素，避免使用双重循环
• x > ans && isPrime(x); 用x>ans 省去Math.max操作。

Java

class Solution {
    public int diagonalPrime(int[][] nums) {
        int n = nums.length;
        int ans = 0;

        for (int i = 0; i < n; i++) {
            int x = nums[i][i];
            if (x > ans && isPrime(x)) { // 用x>ans判断，省去了Math.max的操作
                ans = x;
            }
            int y = nums[i][n - i - 1];
            if (y > ans && isPrime(y)) {
                ans = y;
            }
        }
        return ans;
    }

    public boolean isPrime(int n) {
        for (int i = 2; i * i <= n; i++) {
            if (n % i == 0) {
                return false;
            }
        }
        return n >= 2;
    }
}

3115. 质数的最大距离（20250519更新）

给你一个整数数组 nums。

返回两个（不一定不同的）质数在 nums 中 下标 的 最大距离。

返回最大的质数的距离，首先我们需要判断整数nums[i]是不是质数。

Java

class Solution {
    public int maximumPrimeDifference(int[] nums) {
        int i = 0;
        while (!isPrime(nums[i])) {  // 从左往右找第一个素数
            i++;
        }
        int j = nums.length - 1;  
        while (!isPrime(nums[j])) { // 从右往左找第一个素数
            j--;
        }
        return j - i;
    }

    public boolean isPrime(int x) {
        for (int i = 2; i * i <= x; i++) {
            if (x % i == 0) {  // 如果循环x能整除i，表示i是x的因子，表示x不是质数
                return false;
            }
        } 
        return x >= 2; // 最后判断是否大于等于2， 1不是素数
    }
}

1.2、预处理质数

Changelog

8/20/25, 11:06 AM

View All Changelog

• 4c155-Merge branch 'dev1'on 8/20/25