分享丨【题单】链表、二叉树与回溯（前后指针/快慢指针/DFS/BFS/直径/LCA/一般树）

一、链表

注：由于周赛的链表题可以转成数组处理，难度比直接处理链表低。

带着问题去做下面的题目：

1、在什么情况下，要用到哨兵节点（dummy node）？（需要操作头节点的时候添加dummy节点）

2、在什么情况下，循环条件要写while(node != null)？什么情况下要写while(node.next != null)？（看是否需要判断最后一个节点，如果不处理就用node.next != null，要处理就用node != null.

1.1、遍历链表

1290. 二进制链表转整数（20250804）

Details

给你一个单链表的引用结点 head。链表中每个结点的值不是 0 就是 1。已知此链表是一个整数数字的二进制表示形式。

请你返回该链表所表示数字的 十进制值 。

最高位 在链表的头部。

示例 1：

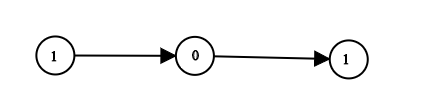
输入：head = [1,0,1]
输出：5
解释：二进制数 (101) 转化为十进制数 (5)

示例 2：

输入：head = [0]
输出：0

提示：

• 链表不为空。
• 链表的结点总数不超过 30。
• 每个结点的值不是 0 就是 1。

如何遍历一个链表？代码框架如下：

// 遍历链表 head
while (head != null) { // 从链表头节点开始向后遍历，直到遇到空节点
    System.out.println(head.val); // 当前节点值
    head = head.next; // 准备遍历下一个节点
}

题目的含义很简单，我们先看10进制字符串“123”如何转化成数字？

• 初始化答案为0
• 0 * 10 + 1 = 1
• 1 * 10 + 2 = 12
• 12*10 + 3 =123

所以对于二进制字符串来说，我们也有相同的实现方式，比如二进制字符串110

• 初始化答案为0
• 0 * 2 + 1 = 1
• 1 * 2 + 1 = 3
• 3 * 2 + 0 = 6

然后我们在结合链表的遍历公式，就能达到一下代码：

Java

class Solution {
    public int getDecimalValue(ListNode head) {
        int ans = 0;
        while(head != null){
            ans = ans * 2 + head.val;
            head = head.next;
        }
        return ans;
    }
}

...

21. 合并两个有序链表

leetcode 第 21 题，合并两个升序的链表，用一个虚拟节点和两个移动指针来解决，判断指针处的节点的大小，插入到虚拟节点后方

class Solution {
    public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
        // 虚拟头结点
        ListNode dummy = new ListNode(-1), p = dummy;
        ListNode p1 = list1, p2 = list2;

        while(p1!=null && p2 !=null){
            if(p1.val > p2.val){
                p.next = p2;
                p2 = p2.next;
            }
            else{
                p.next = p1;
                p1 = p1.next;  // 指针往后移动一位
            }
            p = p.next;  // 移动p
        }
        // 添加上后面没有循环完的节点
        if(p1!=null){
            p.next = p1;
        }
        if(p2!=null){
            p.next = p2;
        }
        return dummy.next;
    }
}

86.分割链表

class Solution {
    public ListNode partition(ListNode head, int x) {
        ListNode dummy1 = new ListNode(-1);  // 两个虚拟头结点
        ListNode dummy2 = new ListNode(-1);

        ListNode p1 = dummy1, p2 = dummy2;  // 两个可移动的节点
        ListNode p = head;
        while(p != null){
            if(p.val >= x){  // 判断节点值的大小，放到对应链表节点后面
                p2.next = p;
                p2 = p2.next;
            }
            else{
                p1.next = p;
                p1 = p1.next;
            }
            ListNode tmp = p.next;  // 原链表指针移动
            p.next = null;
            p = tmp;
        }
        // 合并两个链表
        p1.next = dummy2.next;  // 链接两个链表
        return dummy1.next;  // 返回链表。

    }
}

23. 合并 K 个升序链表

这里用到一个二叉堆的数据结构， 先明白如何用，再说是怎样实现的， 就是使用一个优先级队列来处理，先把条件给出来的链表放到优先级队列里面，后面每次在 pull 出来最小的节点，放到虚拟节点的后面。

class Solution {
    public ListNode mergeKLists(ListNode[] lists) {
        if (lists.length == 0){
            return null;
        }
        ListNode dummy = new ListNode(-1);
        ListNode p = dummy;
        PriorityQueue<ListNode> pq = new PriorityQueue<>(
            lists.length, (a, b)->(a.val - b.val)   // a.val - b.val 最小堆
        );
        // put ListNode head in priorityQueue
        for(ListNode head: lists){
            if(head!= null){  // if head != null
                pq.add(head);
            }
        }
        while(!pq.isEmpty()){  // pq is not empty, pull minest node
            ListNode node = pq.poll();
            p.next = node;
            if(node.next!=null){
                pq.add(node.next);
           }
           p = p.next;
        }
        return dummy.next;
    }
}

1.2、删除节点

视频讲解【基础算法精讲 08】

203. 移除链表元素（20250804）

Details

给你一个链表的头节点 head 和一个整数 val ，请你删除链表中所有满足 Node.val == val 的节点，并返回 新的头节点 。

示例 1：

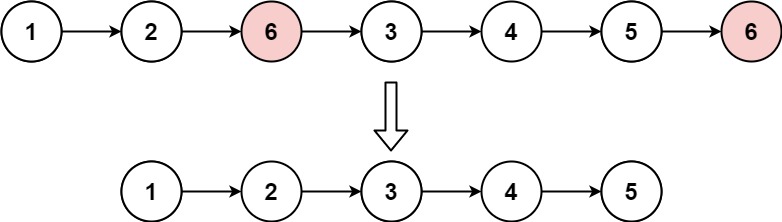
输入：head = [1,2,6,3,4,5,6], val = 6
输出：[1,2,3,4,5]

示例 2：

输入：head = [], val = 1
输出：[]

示例 3：

输入：head = [7,7,7,7], val = 7
输出：[]

提示：

• 列表中的节点数目在范围 [0, 104] 内
• 1 <= Node.val <= 50
• 0 <= val <= 50

套路：

• 要想删除节点node，必须在node的前一个节点执行删除操作。例如链表1->2->3，要想删除节点2，必须在节点1处操作，也就是把节点1的next更新为节点3.
• 如果头节点可能被删除，那么要在头节点之前添加一个哨兵节点，这样我们就无需特判头节点被删除的情况了，从而简化代码逻辑。

算法：

• 初始化哨兵节点dummy，其next为head
• 遍历链表，初始化cur = dummy
• 循环知道cur的下一个节点为空
• 如果cur的下一个节点的值等于val，那么删除下一个节点，把cur.next更新为cur.next.next
• 如果cur的下一个节点不等于val，那么不删除下一个节点，直接更新cur为cur.next

Java

class Solution {
    public ListNode removeElements(ListNode head, int val) {
        // 需要一个dummy node
        ListNode dummy = new ListNode(0, head);
        ListNode cur = dummy;
        // 什么时候判断cur.next != null?
        // 因为需要在前一个节点删除后一个节点，所以最后一个节点不被删除，就不会被删除
        while (cur.next != null) {
            if (cur.next.val == val) {
                cur.next = cur.next.next;
            } else {
                cur = cur.next;
            }
        }
        return dummy.next;
    }
}

1.3、插入节点

2807. 在链表中插入最大公约数（20250804）

Details

给你一个链表的头 head ，每个结点包含一个整数值。

在相邻结点之间，请你插入一个新的结点，结点值为这两个相邻结点值的 最大公约数 。

请你返回插入之后的链表。

两个数的 最大公约数 是可以被两个数字整除的最大正整数。

示例 1：

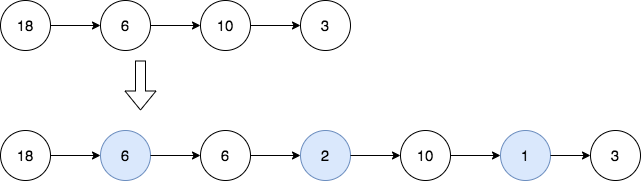
输入：head = [18,6,10,3]
输出：[18,6,6,2,10,1,3]
解释：第一幅图是一开始的链表，第二幅图是插入新结点后的图（蓝色结点为新插入结点）。
- 18 和 6 的最大公约数为 6 ，插入第一和第二个结点之间。
- 6 和 10 的最大公约数为 2 ，插入第二和第三个结点之间。
- 10 和 3 的最大公约数为 1 ，插入第三和第四个结点之间。
所有相邻结点之间都插入完毕，返回链表。

示例 2：

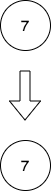
输入：head = [7]
输出：[7]
解释：第一幅图是一开始的链表，第二幅图是插入新结点后的图（蓝色结点为新插入结点）。
没有相邻结点，所以返回初始链表。

提示：

• 链表中结点数目在 [1, 5000] 之间。
• 1 <= Node.val <= 1000

遍历链表，在当前节点cur后面插入gcd节点，同时gcd节点指向cur的下一个节点。

插入后，cur更新为cur.next.next，也就是cur原来的下一个节点，开始下一轮循环，直到cur没有下一个节点。

Java

class Solution {
    public ListNode insertGreatestCommonDivisors(ListNode head) {
        ListNode cur = head;

        // 遍历
        while (cur.next != null) {
            int t = gcd(cur.val, cur.next.val);
            ListNode node = new ListNode(t, cur.next);
            cur.next = node;

            cur = cur.next.next;
        }
        return head;

    }

    // 最小公倍数
    public int lcm(int a, int b) {
        return a * b / gcd(a, b);
    }

    // 最大公约数
    public int gcd(int a, int b) {
        while (a != 0) {
            int t = a;
            a = b % a;
            b = t;
        }
        return b;
    }
}

1.4、反转链表

206. 反转链表（20250810）

Details

给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。

示例 1：

输入：head = [1,2,3,4,5]
输出：[5,4,3,2,1]

示例 2：

输入：head = [1,2]
输出：[2,1]

示例 3：

输入：head = []
输出：[]

提示：

• 链表中节点的数目范围是 [0, 5000]
• -5000 <= Node.val <= 5000

**进阶：**链表可以选用迭代或递归方式完成反转。你能否用两种方法解决这道题？

头插实现反转链表。

比如链表1->2->3，每次遍历的结果：

• 1
• 2 -> 1
• 3 -> 2 -> 1

定义一个cur，指向head， 定义一个pre执行null，每次遍历之后更新cur为pre， pre = cur

当cur指向pre的时候，我们就不知道cur.next的节点了， 所以我们需要先保存下来。

Java

class Solution {
    public ListNode reverseList(ListNode head) {
        ListNode cur = head, pre= null;

        while(cur != null){
            ListNode nxt = cur.next;
            cur.next = pre;
            pre =cur;
            cur = nxt;
        }
        return pre;
    }
}

92. 反转链表 II

Details

给你单链表的头指针 head 和两个整数 left 和 right ，其中 left <= right 。请你反转从位置 left 到位置 right 的链表节点，返回 反转后的链表 。

示例 1：

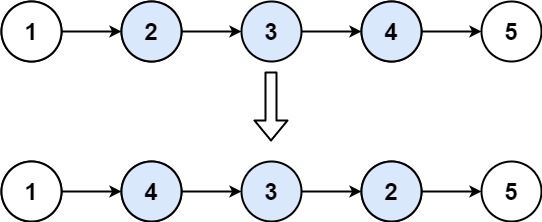
输入：head = [1,2,3,4,5], left = 2, right = 4
输出：[1,4,3,2,5]

示例 2：

输入：head = [5], left = 1, right = 1
输出：[5]

提示：

• 链表中节点数目为 n
• 1 <= n <= 500
• -500 <= Node.val <= 500
• 1 <= left <= right <= n

进阶： 你可以使用一趟扫描完成反转吗？

类似，我们定义一个虚拟头节点dummy，dummy的next就是head，为什么要有一个这样的节点呢？因为当left=1的时候，我们需要操作头节点。

定义一个p节点指向dummy，然后通过p节点遍历到需要反转节点的前一个节点，进行上题反转链表的操作。

反转之后，我们需要把节点串联起来，所以p.next.next 等于待反转链表的下一个节点cur，p.next 等于待反转链表的最后一个节点pre。

Java

class Solution {
    public ListNode reverseBetween(ListNode head, int left, int right) {
        ListNode dummy = new ListNode(0, head);
        ListNode p = dummy;

        for (int i = 0; i < left - 1; i++) {
            p = p.next;
        }
        ListNode cur = p.next, pre = null;
        for (int i = 0; i < right - left + 1; i++) {
            ListNode nxt = cur.next;
            cur.next = pre;
            pre = cur;
            cur = nxt;
        }
        p.next.next = cur;
        p.next = pre;
        return dummy.next;

    }
}

25. K 个一组翻转链表

Details

给你链表的头节点 head ，每 k 个节点一组进行翻转，请你返回修改后的链表。

k 是一个正整数，它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍，那么请将最后剩余的节点保持原有顺序。

你不能只是单纯的改变节点内部的值，而是需要实际进行节点交换。

示例 1：

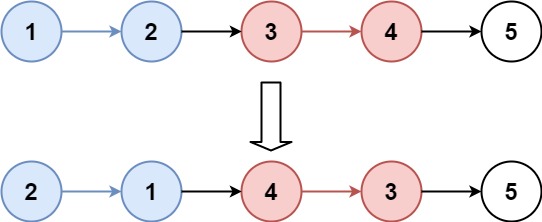
输入：head = [1,2,3,4,5], k = 2
输出：[2,1,4,3,5]

示例 2：

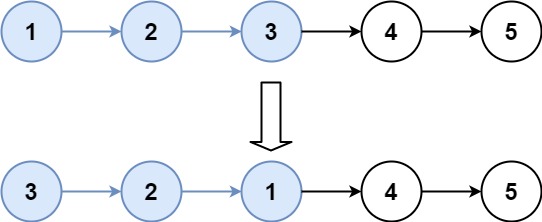
输入：head = [1,2,3,4,5], k = 3
输出：[3,2,1,4,5]

提示：

• 链表中的节点数目为 n
• 1 <= k <= n <= 5000
• 0 <= Node.val <= 1000

**进阶：**你可以设计一个只用 O(1) 额外内存空间的算法解决此问题吗？

理解题目含义比较简单，就是从节点1到n，反转每k个节点，如果最后节点数小于k直接返回。

先获取到节点的个数，当节点个数大于等于k的时候，就反转链表

Java

class Solution {
    public ListNode reverseKGroup(ListNode head, int k) {
        int n = 0;
        for (ListNode cur = head; cur != null; cur = cur.next) {
            n++;
        }

        ListNode dummy = new ListNode(0, head);
        ListNode p0 = dummy;
        ListNode cur = p0.next, pre = null;
        while (n >= k) {
            n -= k;
            // 反转链表的逻辑
            for (int i = 0; i < k; i++) {
                ListNode nxt = cur.next;
                cur.next = pre;
                pre = cur;
                cur = nxt;
            }
            // p0.next 就是待反转链表的最后一个节点。
            ListNode nt = p0.next;
            p0.next.next = cur;
            p0.next = pre;
            p0 = nt;
        }
        return dummy.next;

    }
}

发现一个比较好的求链表长度的代码，直接使用for循环，一行解决，就不用while了， 然后在里面调整节点等于节点.next.

int n = 0;
for (ListNode cur = head; cur != null; cur = cur.next) {
	n++;
}

二、二叉树

学习递归从二叉树开始，晕递归的同学，可以观看灵神的视频讲解，因为我也是跟着灵神学的：看到递归就晕？带你理解递归的本质！【基础算法精讲 09】

一般有三种遍历方式：

• 先序遍历：见2.2自顶向下DFS
• 中序遍历：见2.9二叉搜索树
• 后序遍历：见2.3自底向上的DFS

带着问题去做下面的题目：

1、一般来说，DFS的递归边界是空节点。在什么情况下，要额外把叶子节点作为递归边界？

2、在什么情况下，DFS需要有返回值？什么情况下不需要有返回值？

3、在什么情况下，题目更适合用自顶向下的方法解决？什么情况下适合用自底向上的方法解决？

2.1、遍历二叉树

671. 二叉树中第二小的节点（20250805）

Details

给定一个非空特殊的二叉树，每个节点都是正数，并且每个节点的子节点数量只能为 2 或 0。如果一个节点有两个子节点的话，那么该节点的值等于两个子节点中较小的一个。

更正式地说，即 root.val = min(root.left.val, root.right.val) 总成立。

给出这样的一个二叉树，你需要输出所有节点中的 第二小的值 。

如果第二小的值不存在的话，输出 -1 。

示例 1：

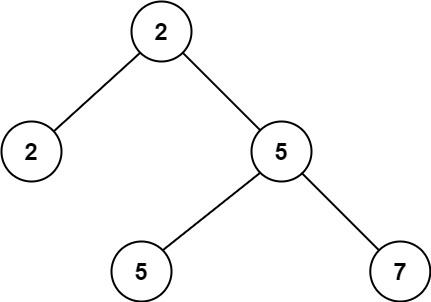
输入：root = [2,2,5,null,null,5,7]
输出：5
解释：最小的值是 2 ，第二小的值是 5 。

示例 2：

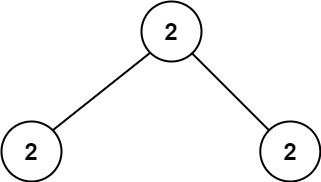
输入：root = [2,2,2]
输出：-1
解释：最小的值是 2, 但是不存在第二小的值。

提示：

• 树中节点数目在范围 [1, 25] 内
• 1 <= Node.val <= 231 - 1
• 对于树中每个节点 root.val == min(root.left.val, root.right.val)

理解题目还是比较简单的，就是遍历之后找到次小值。

存在重复的元素，遍历可以考虑使用集合来保存遍历的结果。

找到次小值的方法有多种，可以通过排序找次小值，复杂度为O(nlogn)；也可以使用经典的两个变量 & 一次遍历的方式找到次小值，复杂度为O(n)。

Java

class Solution {
    public int findSecondMinimumValue(TreeNode root) {
        Set<Integer> ans = new HashSet<>();

        dfs(root, ans);
        if (ans.size() < 2) {
            return -1;
        }
        int firstMin = Integer.MAX_VALUE;
        int secondMin = Integer.MAX_VALUE;
        // 经典两个变量&一次遍历，找到次小值。
        // 如果小于最小值，就更新最小值和次笑值；如果小于次小值，就更新次小值。
        for (int x : ans) {
            if (x < firstMin) {
                secondMin = firstMin;
                firstMin = x;
            } else if (x < secondMin) {
                secondMin = x;
            }
        }
        return secondMin;
    }

    public void dfs(TreeNode root, Set<Integer> ans) {
        if (root == null) {
            return;
        }
        ans.add(root.val);
        dfs(root.left, ans);
        dfs(root.right, ans);
    }
}

2.2、自顶向下DFS（先序遍历）

在 【递】的过程中维护值。（有些题自顶向下和自底向上都可以，BFS也可以）

104. 二叉树的最大深度（20250326）

Details

给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：3

示例 2：

输入：root = [1,null,2]
输出：2

提示：

• 树中节点的数量在 [0, 104] 区间内。
• -100 <= Node.val <= 100

参考灵神的题解：【视频讲解】让你对递归的理解更上一层楼！（Python/Java/C++/C/Go/JS/Rust）

这道题从2020年开始就有提交，到现在2025年，终于有了不一样的理解。

我们需要知道什么是二叉树的最大深度，就是从跟节点到最下方叶子节点经过的节点个数为二叉树的最大深度。

自顶向下DFS，知识点：

• 自顶向下递归不需要返回值，需要额外维护结果值

对于这道题来说，因为我们遍历到一个节点，不知道这个节点的高度，所以需要维护一个节点的高度，然后每次进入节点就比较当前节点的高度，与最大高度的大小，更新最大高度。

自顶向下

class Solution {
    int max;

    public int maxDepth(TreeNode root) {
        // 自顶向下（不需要返回值）
        dfs(root, 0);
        return max;
    }

    public void dfs(TreeNode root, int cur) {
        if (root == null) {
            return;
        }
        cur += 1;
        max = Math.max(max, cur);
        dfs(root.left, cur);
        dfs(root.right, cur);
    }
}

2.3 自底向上 DFS（后序遍历）

在【归】的过程中计算。

104. 二叉树的最大深度（20250805）

还是二叉树的最大深度这道题，使用自底向上的思路的话，就是要维护每个节点的返回值

自底向上，知识点：

• 自底向上，需要一层一层反上去，所以需要一个返回值。
• 假设每次遍历节点都正确返回数据。

关于题目，需要注意的是根节点，分别求到左子树的最大深度和右子树的最大深度之后，我们需要加上根节点的高度1.

Java

class Solution {
    public int maxDepth(TreeNode root) {
        // 自底向上
        return dfs(root);
    }

    // 返回这个节点高度，假设递归都正确返回
    public int dfs(TreeNode root) {
        if (root == null) {
            return 0;
        }

        int lv = dfs(root.left);
        int rv = dfs(root.right);
        return Math.max(lv, rv) + 1;
    }
}

2.7、回溯

257. 二叉树的所有路径（20250405）

给你一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。

叶子节点 是指没有子节点的节点。

自顶向下递归求解

class Solution {
    List<String> ans = new ArrayList<>();

    public List<String> binaryTreePaths(TreeNode root) {
        dfs(root, "");
        return ans;
    }
    // 通过递归求解
    void dfs(TreeNode node, String path) {
        if (node == null) {
            return;
        }
        path += node.val;  // 自顶向下递归，每次进入节点就添加到路径里面

        if (node.left == node.right) {  // 判断叶子节点
            ans.add(path);
        }
        path += "->";  // 最后在用->关联
        dfs(node.left, path);
        dfs(node.right, path);
    }
}

回溯

class Solution {
    List<String> ans = new ArrayList<>();

    public List<String> binaryTreePaths(TreeNode root) {
        List<String> path = new ArrayList<>();
        dfs(root, path);
        return ans;
    }

    // 递归回溯解
    void dfs(TreeNode node, List<String> path) {
        if (node == null) {
            return;
        }
        path.add(String.valueOf(node.val));
        if (node.left == node.right) {
            ans.add(String.join("->", path));
        } else {
            dfs(node.left, path);
            dfs(node.right, path);
        }
        path.remove(path.size() - 1);
    }
}

可能你会问，什么时候使用递归？什么时候使用回溯？

递归是一个函数不断调用自身，通常用于把大问题拆解成小问题并逐步求解；回溯是在递归的基础上，尝试所有可能的解，并在不满足条件是回退，撤销上一步决策。

2.9、二叉搜索树

一般使用中序遍历，因为中序遍历出来的结果是有序的。

验证二叉搜索树【基础算法精讲 11】

98. 验证二叉搜索树（20250729）

Details

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

• 节点的左子树只包含 严格小于 当前节点的数。
• 节点的右子树只包含 严格大于 当前节点的数。
• 所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

输入：root = [2,1,3]
输出：true

示例 2：

输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

提示：

• 树中节点数目范围在[1, 104] 内
• -231 <= Node.val <= 231 - 1

这里讲一下通过前序遍历和中序遍历来解决的思路。

对于前序遍历，我们在访问节点的时候，传入这个节点值的取值范围，比如下面函数：

boolelan dfs(TreeNode root, long left, long right){}，判断是否在范围中，同时判断节点的左子树是否满足二叉搜索树，节点的右子树是否是二叉搜索树。

问：为什么Java等语言需要用到Long类型？题目给出的范围不是int类型吗？

虽然题目给出的是int类型，但是开始递归的时候，left需要比所有节点都小，right需要比所有节点都大，如果节点刚是是int的最大值或者最小值的话，就比较不了，所以用long类型。

对于中序遍历，可以把二叉搜索树看成一个有序的数组，怎么判断一个数组是否有序？比较相邻元素的大小即可。

Java

class Solution {
    public boolean isValidBST(TreeNode root) {
        return dfs(root, Long.MIN_VALUE, Long.MAX_VALUE);
    }
    public boolean dfs(TreeNode root, long left, long right) {
        if (root == null) {
            return true;
        }
        long x = root.val;
        return left < x && x < right && dfs(root.left, left, x) && dfs(root.right, x, right);
    }
}

Java 中序遍历

class Solution {
    long pre = Long.MIN_VALUE;

    public boolean isValidBST(TreeNode root) {
        if (root == null) {
            return true;
        }
        // 中序遍历，12345
        if (!isValidBST(root.left)) {
            return false;
        }
        long x = root.val;
        if (x <= pre) {
            return false;
        }
        pre = x; // 自动转形
        return isValidBST(root.right);
    }
}

2.13 二叉树 BFS

104. 二叉树的最大深度（20250326）

Details

给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：3

示例 2：

输入：root = [1,null,2]
输出：2

提示：

• 树中节点的数量在 [0, 104] 区间内。
• -100 <= Node.val <= 100

BFS有三种写法，一种就是最简单的，把节点存进去然后取出来遍历，但是这一种没有办法记录层数；第二种就是通过一个for循环来记录每一层，相当于每层的权重是1；还有第三种就是节点维护自己的层级（权重）。

Java

class Solution {
    int depth = 0;

    public int maxDepth(TreeNode root) {
        bfs(root);
        return depth;
    }

    void bfs(TreeNode root) {
        if (root == null) {
            return;
        }
        Queue<TreeNode> q = new LinkedList<>();
        q.offer(root);

        while (!q.isEmpty()) {
            int sz = q.size();
            for (int i = 0; i < sz; i++) {
                TreeNode node = q.poll();
                if (node.left != null) {
                    q.offer(node.left);
                }
                if (node.right != null) {
                    q.offer(node.right);
                }
            }
          	// 可以在这里记录层数
          	// 也可以在循环里面保存元素值，这样就能得到遍历的结果
            depth++;
        }
    }
}

三、一般树

3.1、遍历

2368. 受限条件下可到达节点的数目（20250729）

Details

现有一棵由 n 个节点组成的无向树，节点编号从 0 到 n - 1 ，共有 n - 1 条边。

给你一个二维整数数组 edges ，长度为 n - 1 ，其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条边。另给你一个整数数组 restricted 表示 受限 节点。

在不访问受限节点的前提下，返回你可以从节点 0 到达的 最多 节点数目*。*

注意，节点 0 不 会标记为受限节点。

示例 1：

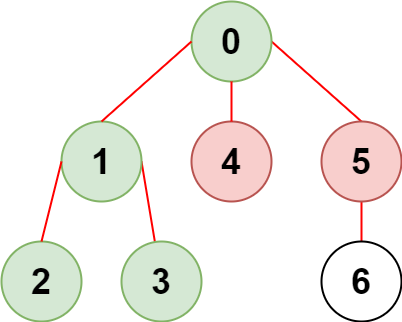
输入：n = 7, edges = [[0,1],[1,2],[3,1],[4,0],[0,5],[5,6]], restricted = [4,5]
输出：4
解释：上图所示正是这棵树。
在不访问受限节点的前提下，只有节点 [0,1,2,3] 可以从节点 0 到达。

示例 2：

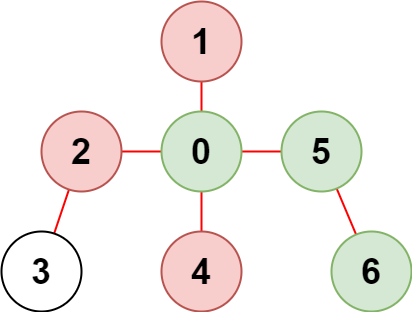
输入：n = 7, edges = [[0,1],[0,2],[0,5],[0,4],[3,2],[6,5]], restricted = [4,2,1]
输出：3
解释：上图所示正是这棵树。
在不访问受限节点的前提下，只有节点 [0,5,6] 可以从节点 0 到达。

提示：

• 2 <= n <= 105
• edges.length == n - 1
• edges[i].length == 2
• 0 <= ai, bi < n
• ai != bi
• edges 表示一棵有效的树
• 1 <= restricted.length < n
• 1 <= restricted[i] < n
• restricted 中的所有值 互不相同

开始想的是使用刚学的图的遍历来解（最后也是用这种方法），但是在第二遍提交的时候，OOT了，所以参考灵神修改了一下代码，就是边两端的节点，只有都不受限制的时候，才添加到树上面。

最后通过遍历访问数组，统计被访问的节点个数，就是结果。

Java

class Solution {
    public int reachableNodes(int n, int[][] edges, int[] restricted) {
        boolean[] rst = new boolean[n];
        for (int x: restricted) {
            rst[x] = true;
        }
        List < Integer > [] g = new ArrayList[n];
        Arrays.setAll(g, x -> new ArrayList < > ());

        for (int[] e: edges) {
            int x = e[0], y = e[1];
            // 只有值不都不受限制，才添加到树上
            if (!rst[x] && !rst[y]) {
                g[x].add(y);
                g[y].add(x);
            }
        }

        boolean[] visited = new boolean[n];
        dfs(0, g, visited, rst);

        int ans = 0;
        for (boolean b: visited) {
            if (b) {
                ans++;
            }
        }
        return ans;
    }

    private void dfs(int x, List < Integer > [] g, boolean[] visited, boolean[] rst) {
        visited[x] = true;
        for (int y: g[x]) {
            if (!visited[y] && !rst[y]) {
                dfs(y, g, visited, rst);
            }
        }
    }
}

也可以直接通过dfs递归，直接将结果返回回去。

    private int dfs(int x, List<Integer>[] g, boolean[] visited,  boolean[] rst) {
        int cnt = 1;
        visited[x] = true;
        for (int y : g[x]) {
            if (!visited[y] && !rst[y]) {
                int num = dfs(y, g, visited, rst);
                cnt += num;
            }
        }
        return cnt;

四、回溯

4.1、入门回溯

回溯算法套路①子集型回溯【基础算法精讲 14】

17. 电话号码的字母组合（20250405）

Details

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

用一个path数组记录路径上的字母。

回溯三问：

• 当前操作？枚举path[i]要填入的字母
• 子问题？构造字符串>=i的部分
• 下一个子问题？构造字符串>=i+1的部分

Java

class Solution {
    static final String[] MAPPING = new String[] { "", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz" };

    List<String> ans = new ArrayList<>();
    char[] digits;
    char[] path;

    public List<String> letterCombinations(String digits) {
        int n = digits.length();
        if (n == 0) {
            return List.of();
        }
        this.digits = digits.toCharArray();
        path = new char[n];
      
        dfs(0);
        return ans;
    }

    void dfs(int i) {
        // 递归边界
        if (i == digits.length) {
            ans.add(new String(path));
            return;
        }
        // 枚举第i个字母是什么
        for (char c : MAPPING[digits[i] - '0'].toCharArray()) {
            path[i] = c;
            dfs(i + 1);
        }
    }
}

4.2、子集型回溯

有【选或者不选】和【枚举选那个】两种写法。

也可以用二进制枚举做。

78. 子集（20250405）

Details

给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。

解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。

方法一：输入的视角（选或者不选）

class Solution {
    List<List<Integer>> ans = new ArrayList<>();
    List<Integer> path = new ArrayList<>();
    int[] nums;

    public List<List<Integer>> subsets(int[] nums) {
        this.nums = nums;
        dfs(0);
        return ans;
    }

    // 从输入的角度来解（就是选与不选的却别）
    void dfs(int i) {
      	// 递归边界条件
        if (i == nums.length) {
            ans.add(new ArrayList<>(path));
            return;
        }
        // 不选
        dfs(i + 1);

        // 选
        path.add(nums[i]);
        dfs(i + 1);
        path.remove(path.size() - 1);

    }
}

方法二：答案的视角（枚举选哪个）

class Solution {
    List<List<Integer>> ans = new ArrayList<>();
    List<Integer> path = new ArrayList<>();
    int[] nums;

    public List<List<Integer>> subsets(int[] nums) {
        this.nums = nums;
        dfs(0);
        return ans;
    }

    void dfs(int i) {
        // 由于子集的长度没有约束，所以每个长度都可以是答案，所以每次递归都需要记录一下答案
        ans.add(new ArrayList<>(path));
        if (i == nums.length) {
            return;
        }
        // 枚举答案的第一个数选谁，第二个数选谁？
        for (int j = i; j < nums.length; j++) {
            path.add(nums[j]);
            dfs(j + 1);
            path.remove(path.size() - 1);
        }
    }
}

Changelog

8/20/25, 11:06 AM

View All Changelog

• 4c155-Merge branch 'dev1'on 8/20/25